化归法在最值问题中的应用
南京市宁海中学分校 蒋敏
我们经常用代数方法求一些最值问题,但有时也会遇到麻烦,有的过程繁琐,
有的方法不明,无从下手.此时,如果我们善用化归法,从几何的角度分析,充
分利用图形的特征,便能轻松解题.
所谓化归,从字面上可理 解为转化和归结的意思.化归法指的是把待解决
的问题,通过某种转化过程,归结到一类已经解决或比较容易解决的问题中去,最终求得原问题之解答的一种手段和方法.在这个过程中,关键是如何转化,转化的方法有多种,其中有一种很重要的转化途径是数形结合,即通过图解或绘制图象的方法来求解正确答案.下面例说用化归法求最值问题.
1求线段长度之和的最值
1.1两个定点一个动点
如图1(1),在菱形ABCD中,AB=4a,点E是BC的中点,点P在BD上,则PE+PC的最小值是多少?
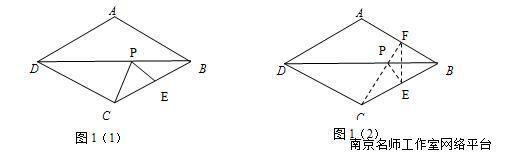
思路分析:在P, E,C三个点中,有两个定点C, E,一个动点P.所以线段PE和PC的长度都不确定.要求PC+PE的最小值,可以把PE和PC 转化到同一条直线上.如图1(2),利用菱形是轴对称图形,BC的中点E关于BD的对称点F一定落在AB的中点上,得PE=PF,那么只要求出PF +PC的最小值即可. 根据两点间线段最短的原理,连结CF交BD于点P,当点P位于如图位置时,PE+PC最小.问题就转化成求CF的长度了.
在RtCBF中,BC=4a,可得CF=,即答案为
变式:求的最小值.
利用“数形迁移”策略,建立直角坐标系,将代数结构转化成几何结构.此问题可转化为:在x轴上找一点,使它到两点(3,1),(-3,5)的距离和最短. 用上题的方法可得答案为![]() .
.
1.2一个定点两个动点
等腰直角三角形ABC中,AB=2a,AD是∠BAC的角平分线,在AD上找一点P,过P作PE//BC,使PB+PE最短,此时最短距离是多少?
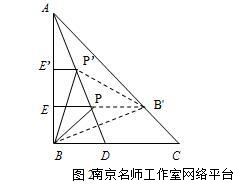
思路分析:如图,在P, B, E三个点中,有一个定点B和两个动点P和E.先在AD上任取一点P’,过点P’作P’E’//BC,再取点B关于AD的对称点B’,得P'B=P'B',则P’B+P’E’=P’B’+P’E’.要使P’B+P’E’最短,只要P’B’+P’E’最短.过B’作B’E//BC交AD于点P,由两点之间线段最短可知,当点P位于如图位置时, B'P+PE<B'P'+P'E'.此时PB+PE最小,最小值即为B'E的长度.
因为B'与B关于AD对称,所以AB'=AB=2a,在等腰直角三角形AEB'中,斜边AB'=2a,由勾股定理可得B'E=![]() .
.
变式:求三条线段长度之和的最小值
如图3(1),, 角内有一点P,PO=5,在角的两边上有两点M,N(均不同于O点),求周长的最小值.
|
|
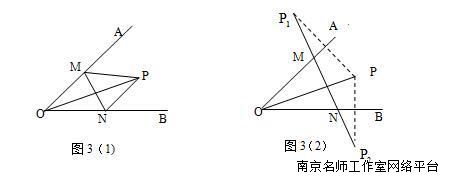
思路分析:在这个问题中,点P为定点,M和N都是动点,所以三条线段PM,PN,MN的长度都不确定,那么如何确定M,N两点的位置才能使的周长取到最小值呢?如图3(2),分别取P点关于射线OA和OB的对称点和,则PM=,,则的周长=+,所以的周长的最小值就是线段的长度.利用轴对称性,可知为等腰直角三角形,=,即的周长的最小值为.
2.求线段长度之差的最值
如图4所示,两点A,B在直线MN外的两侧,A到MN的距离AC=8 ,B到MN的距
离BD=5, CD=4 ,P在直线MN上运动,求|PA-PB|的最大值.
|
|
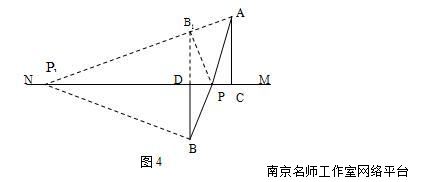
思路分析:分类讨论,当PA>PB时,|PA-PB|=PA-PB;当PA<PB时,|PA-PB|=PB-PA.只要先研究其中一种即可.如图4,当PA〉PB时,方法是将PA和PB转化到同一个三角形中. A,B两点在直线MN外的两侧,取B关于MN的对称点,则PB=,PA-PB=PA-.在三角形A中, 根据AP-<,所以连结并延长交MN于点,此时PA-PB最大,最大值为.通过简单计算,可得长度为5.
3.求线段长度之商的最值
如图5所示,以点P(2,0)为圆心, eq \r(3) 为半径作圆,点M(a,b) 是⊙P上
的一点,则 eq \f(b,a)的最大值是 ▲ .
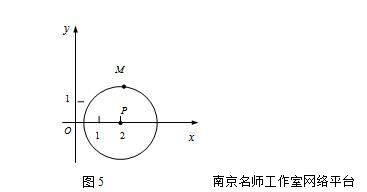
思路分析1:代数法
由已知条件可得方程,
变形得:;要求 eq \f(b,a)的最大值,可先求的最大值.(a0),令,则 ,化简得关于a的一元二次方程(m-1),再根据根的存在条件可得,≥0,得m3,即的最大值为3, 则 eq \f(b,a)的最大值是 eq \r(3) .
思路分析2:几何法
把的值转化成∠MOP的正切值,要使的值最大,只要使 tan∠MOP的值最大,而tan∠MOP的值随∠MOP的增大而增大。何时∠MOP什么时候最大呢?通过图形的特征可知,当OM和⊙P相切时,且点M在第一象限时,的值最大.此时,tan∠MOP==,所以答案是 eq \r(3) .
相比之下,用数形结合的方法更简便.
4.求角度的最值
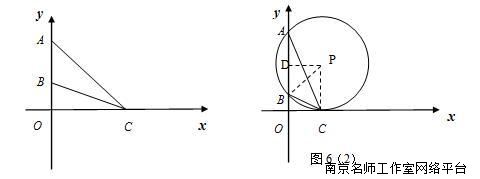
如图6所示,在平面直角坐标系中,在y轴的正半轴上给定两点A(0,3)和B(0,1),试在x的正半轴上求点C,使∠ACB取最大值.
思路1:要求∠ACB的最大值, ∠ACB=∠ACO-∠BCO,而∠ACO与∠BCO都是
变化的
思路2:也可先求tan∠ACB的最大值,即tan(∠ACO-∠BCO)的最大值,初中阶段
目前没有公式可用
两种思路都有难度.
思路3:用数形结合的方法,从图形的角度分析,何时∠ACB最大?.A、B、C三个点中,两个点不动,第三个点在动.联想三角形的外角大于任意一个不相邻的内角.方法是把∠ACB转化成圆周角.如图6(2),在一个圆中,同弧所对的圆周角大于圆外角,小于圆内角.所以要使∠ACB最大,只要使x轴上除C点以外的其他点都在过A,B,C三点的圆外即可.也就是说,过A,B两点的圆与 x轴相切的切点就是所求的C点.
过点P作PD⊥AB交AB于点D,由垂径定理得AD=DB,设半径为R,则3-R=R-1,得R=2.在![]() 中,BP=2,BD=1,由勾股定理得DP= eq \r(3) ,从而求得点C的坐标是
中,BP=2,BD=1,由勾股定理得DP= eq \r(3) ,从而求得点C的坐标是![]() .
.
在解决最值问题时,首先要有化归的意识,其次要有化归的方法.我们要加
强空间观念,活用几何定理,善用数形结合法,在数量关系和空间形式两大领域内遨游,从而求得最佳解题方法.
地址:南京市龙江小区港龙园1号宁海中学分校 邮编:210036
电话:13951978232 邮箱:jm_njjh@163.com















